Pythagorean Theorem and Carpentry
Modern carpentry work is so much easier when the Pythagorean Theorem is applied to the task at hand. Roof framing, squaring walls, and foundations rely on this basic principle of mathematics.
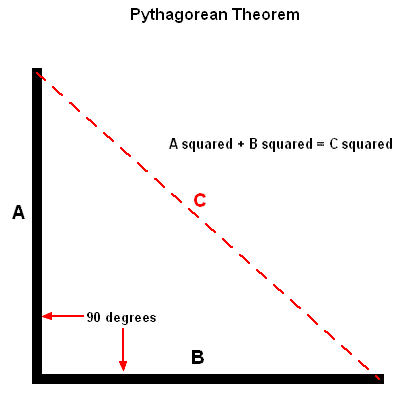
Basics of the Theorem
In geometry this theorem states,
in a right triangle the square of the hypotenuse equals the sum of the
squares of the other two sides. In a right triangle one angle equals 90 degrees. The hypotenuse is on the opposite side of the right triangle.
Here is the formula for the Pythagorean Theorem. a squared + b squared = c squared In this formula, c represents the length of the hypotenuse, a and b are the lengths of the other two sides. If two sides of a right triangle are known, you can substitute these values in the formula to find the missing side.
Squaring Buildings with the Pythagorean Theorem
When laying out concrete footings for a new building, the Pythagorean
Theorem is the most accurate method available for making square 90 degree angles. It is the same as the old 3 – 4 – 5 carpentry trick, only more precise, because the exact corners can be located.
Normally in carpentry points a and b are known so all you have to do is solve for c. Here is a neat little calculator that you can use to simplify the math.
( a2 + b2 = c2 )
2 =
Let us say you have a dimension of 16′ x 14′ that you need to square up. If you
enter 16 and 14 into the calculator and press solve you will get an answer of 21.2602916254693.
This number isn’t of much use until we convert it to feet and inches.
Below are the steps needed to convert this to feet and inches using a regular calculator.
- Drop the 21 which represents 21 feet.
- Round the decimal point to four places, so .2602916254693 becomes .2603.
- Enter .2603 into calculator and multiply by 12 – .2603 x 12 = 3.1236 inches.
- Enter .1236 into calculator and multiply by 16 – .1236 x 16 = 1.9776 16’ths of an inch.
- Round 1.9776 up to 2/16 or 1/8″.
So the answer is 21′ 3 1/8″.
Using a Regular Calculator
The Pythagorean Theorem can also be used with a regular calculator provided it
is equipped with a square root function key. Below are the sequence of keystrokes, using
the 16′ x 14′ example.
16 x = 256 MS (Memory Save) 14 x = 196 + MR (Memory Recall) =
452 sqrt (Square Root) 21.2602916254693
Here are a few practice problems, if you would like to try you’re hand?
32′ x 42′ = Answer
44′ x 24′ = Answer
62′ x 28′ = Answer
If you got all these right, congratulations, you now have a new carpentry trick up your sleeve.
Construction Master Calculator
This calculator simplifies this process by leaps and bounds over the two previously mentioned
methods. Here are the only keystrokes needed for the same results. 16 Feet Rise
14 Feet Run Diag 21′ 3 1/8″.
Here is how the theory is applied to roof framing.

Pythagorean Theorem Origins
Around 2000 B.C. the ancient Egyptians needed a way to lay out square corners
for their fields. They took a length of rope knotted into 12 equal sections and stretched the rope around
three stakes arranged in a triangle. When they had 3 lengths between two stakes, 4 lengths
between the next two, and 5 lengths back to the starting point the hypotenuse of the right
triangle was formed.
A man named Pythagoras became famous for formulating the Theorem, however
it was certainly known earlier. He was a Greek philosopher and mathematician born
around 530 B.C. He founded a brotherhood called the Pythagoreans in Crotona, Italy,
among the aristocrats of that city. The townspeople became suspicious of the brotherhood
and killed most of its members in a political uprising. It is not known if he fled the
city before the uprising or was killed in it.
Links to Related Carpentry Pro Framer Pages